2010: ROMA – ACCADEMIA NAZIONALE DEI LINCEI "X GIORNATA DELL’ACQUA"
Stabilizzazione superficiale di versanti con la tecnologia dei PRATI ARMATI®: implementazione di un modello di calcolo per la valutazione del coefficiente di sicurezza.
IL 22-03-2010 l’Accademia nazionale dei Lincei ha organizzato la X giornata dell’acqua durante la quale è stato presentato un modello di calcolo per la valutazione del coefficiente di sicurezza per la stabilità di un versante con l’apporto dei PRATI ARMATI®, piante erbacee a radicazione profonda, sottile e resistente.
Posizione del problema
Fenomeni superficiali di instabilità dei versanti ed eventuali fenomeni di erosione possono essere efficacemente contenuti mediante l’impianto di coltri vegetali con apparato radicale relativamente profondo. Nel 1999 si costituiva in Italia la società PRATI ARMATI® che ha sviluppato un’innovativa tecnologia “verde” per fronteggiare i fenomeni di erosione del suolo, di cui detiene l’esclusiva mondiale. Tale tecnologia appare ad oggi parimenti efficiente nel contenere fenomeni di instabilità di coltri superficiali per diverse tipologie di depositi interessati. I risultati ottenuti in diversi cantieri in Italia ed all’estero ne sono testimonianza. Nel corso degli anni, PRATI ARMATI® ha raccolto per molte specie vegetali una mole rilevante di dati relativi, ad esempio, alle dimensioni e alla resistenza a trazione delle radici, alla densità e profondità massima di radicazione, alla capacità di traspirazione. Da studi accurati e approfonditi ogni anno emergono in media 2-3 nuove specie da utilizzare con successo, garantendo così la possibilità di estendere questo tipo di interventi a situazioni molto diverse fra loro, per condizioni climatiche, topografiche, geologiche, idrogeologiche e geotecniche.
Contributo dell’inerbimento alla stabilità dei versanti
L’inerbimento di pendii e versanti con la tecnica dei, PRATI ARMATI® può indurre numerosi effetti sulle condizioni idrauliche e meccaniche dei terreni inerbiti, che a loro volta si riflettono sulle condizioni di equilibrio del pendio stesso. Uno di questi effetti, di natura meccanica, è evidentemente attribuibile alle radici. L’incremento di resistenza a taglio del terreno per effetto delle radici è infatti da tempo riconosciuto e studiato (Vidal, 1969; Schlosser e Long, 1974), e tale effetto è attualmente schematizzato ed implementato in un apposito codice di calcolo di proprietà PRATI ARMATI®.
Altri effetti, di natura prevalentemente idraulica, non sono allo stesso modo studiati ed implementati. Per questa ragione, recentemente, è stato avviato uno studio il cui oggetto primario è l’approfondimento e l’implementazione del meccanismo secondo il quale l’inerbimento con PRATI ARMATI® può ridurre significativamente il contenuto d’acqua del terreno, sia inibendo l’infiltrazione di acqua meteorica che attraverso l’assorbimento di acqua da parte delle radici. Questa riduzione del contenuto d’acqua, e del grado di saturazione, incrementa a sua volta la resistenza a taglio del terreno e migliora le condizioni di equilibrio del pendio.
Obbiettivo dello studio
L’obiettivo dello studio è quindi quello di valutare il suddetto meccanismo, per lo schema di pendio indefinito, sia da un punto di vista fenomenologico che quantitativo. Il problema è evidentemente complesso, dal momento che i fenomeni in gioco sono molteplici ed il loro studio richiede competenze specifiche in diversi settori, dall’agronomia, alla fisica dei terreni, all’idraulica e non ultimo all’ingegneria geotecnica. Una rappresentazione schematica di insieme del problema in studio è rappresentata in Figura 1.
Figura 1. Rappresentazione schematica del problema in esame
Da un punto di vista analitico-numerico, le condizioni al contorno in termini di flusso dipendono dall’equazione di bilancio delle masse, tenendo conto dei fenomeni di evaporazione al suolo, evapotraspirazione delle radici, infiltrazione di acqua nel terreno, ruscellamento lungo il pendio. Nel terreno non saturo, le equazioni che governano il flusso della fase liquida e della fase aeriforme (equazione di continuità e legge di Darcy), sotto alcune ipotesi, conducono alla ben nota equazione di Richards (1931). La soluzione di questa equazione fornisce l’andamento del contenuto d’acqua, q (z, t), in funzione della profondità (z) e del tempo (t). Note le proprietà di ritenzione idrica del terreno (curva caratteristica, q (s)), è quindi possibile ricavare il profilo di suzione, s(z). Da quest’ultimo, infine, adottando un criterio di rottura che tenga conto della parziale saturazione, è possibile valutare la resistenza a taglio del terreno (es.: Fredlund et al., 1996; Rassam e Cook, 2002; Vanapalli et al., 1996) e le condizioni di equilibrio del pendio. Allo stato attuale, alcuni aspetti sono ancora in fase di studio e sono trattati in modo semplificato.
Descrizione del modello di calcolo
Il modello di calcolo è strutturato in VISUAL BASIC – EXCEL e si articola in fogli di lavoro consecutivi, coerentemente con i passi logici dell’algoritmo di calcolo. In questo modo, i risultati dei passi intermedi del calcolo possono essere visualizzati ed esaminati. L’applicativo costituisce lo sviluppo del software originariamente formulato da PRATI ARMATI®.
Il codice di calcolo
Il codice, denominato PRATI_ARMATI@UNIVPG è così articolato:
-
Inserimento dati terreno.
Si richiede all’utente di inserire i parametri geometrici (inclinazione del pendio, eventuale profondità della superficie libera), fisici (es.: peso dell’unità di volume), idraulici (es.: contenuto d’acqua a saturazione, proprietà di ritenzione idrica, conducibilità idraulica) e meccanici (coesione, angolo di attrito del terreno) che definiscono completamente il modello di pendio indefinito.
-
Inserimento dati specie vegetazione.
A partire dall’elevata mole di dati sperimentali desunti da prove di trazione su diverse tipologie di radici (v. Rapporto PRATI ARMATI®, 2009), occorre dapprima definire i valori caratteristici della specie selezionata, in termini di diametro delle radici, D (Dmin, Dmax, Dmedio) ed i corrispondenti valori della resistenza a trazione unitaria, Tr. Successivamente, occorre selezionare la funzione di distribuzione statistica dei diametri da adottare, tra quelle proposte (es.: normale, triangolare, lognormale). L’inserimento di questa serie di dati è finalizzato alla stima di un valore rappresentativo dell’incremento di resistenza al taglio offerto dalle radici, DSr, secondo l’approccio proposto da Bischetti et al.(2001) e Bonfanti & Bischetti (2001):
L’applicativo PRATI_ARMATI@UNIVPG consente di costruire la distribuzione dei diametri in base alla legge indicata, sia partendo dai valori forniti per ogni specie da PRATI ARMATI® (e impostati come di default nell’applicativo), sia consentendo una personalizzazione da parte dell’utente.
Occorre poi definire una seconda serie di dati per la singola specie, con lo scopo di valutare i parametri, prevalentemente di natura empirica, che definiscono le leggi dell’evapotraspirazione (Allen et al., 1998; Feddes, 1987), la capacità di intercettamento della precipitazione da parte della porzione epigea, in funzione delle diverse fasi di crescita, l’effetto indotto sui fenomeni di run-off . Dalle equazioni risolventi che controllano tali fenomeni e dalla soluzione numerica dell’equazione di Richards, è possibile stimare il profilo di contenuto d’acqua volumetrico nel terreno in condizione di parziale saturazione per ogni istante temporale all’interno del volume di terreno radicato.
Incremento della resistenza a taglio del terreno
Il codice di calcolo consente a questo punto di calcolare la resistenza a taglio del terreno (tf), tenendo conto delle effettive condizioni di saturazione. In PRATI_ARMATI@UNIVPG si è adottato il criterio di resistenza proposto da Vanapalli et al. (1996), secondo cui:
Nell’equazione 2 la suzione s è determinata a partire dal contenuto d’acqua volumetrico mediante una delle equazioni proposte per le curva caratteristica (Van Genuchten, 1980; Fredlund & Xing, 1994).
Input Area
Un’altra grandezza fondamentale nella caratterizzazione del contributo stabilizzante delle radici è il rapporto di radicazione, AR/A. Considerata la natura prevalentemente fittonante delle specie PRATI ARMATI®, in genere il rapporto di radicazione si mantiene praticamente costante con la profondità. Tuttavia, nel modello è consentito scegliere una tra tre diverse funzioni AR/A (z) (costante, lineare, legge di potenza), che in tutti i casi è caratterizzata da un andamento decrescente con la profondità.
Incremento di resistenza a taglio, offerto dalle radici
Il contributo meccanico offerto dalle radici alla resistenza a taglio del terreno è di tipo coesivo (Gray & Ohashi, 1996). Tale contributo risulta direttamente proporzionale alla resistenza a trazione delle radici ed al rapporto di radicazione. Si precisa che nell’equazione 1, il coefficiente di proporzionalità 1.15 è un valore sperimentalmente accertato che consente di tenere conto della configurazione geometrica iniziale delle radici rispetto alla potenziale superficie di scorrimento del pendio. Nel codice PRATI_ARMATI@UNIVPG, il calcolo di DSr può anche essere condotto avvalendosi dell’equazione proposta da Waldron (1977):
In alcuni casi, questo secondo approccio appare più cautelativo nei confronti delle condizioni di sicurezza del pendio. Inoltre, il modello di calcolo permette di valutare l’incremento di resistenza al taglio offerto dalle radici DSr, anche nei riguardi dello stato limite di sfilamento della radice dal terreno, che talvolta può risultare più critico di quello a trazione. In tutti i casi, il contributo DSr è ridotto cautelativamente del 50%, per tenere conto del fatto che non tutte le radici mobilitano contestualmente la massima resistenza.
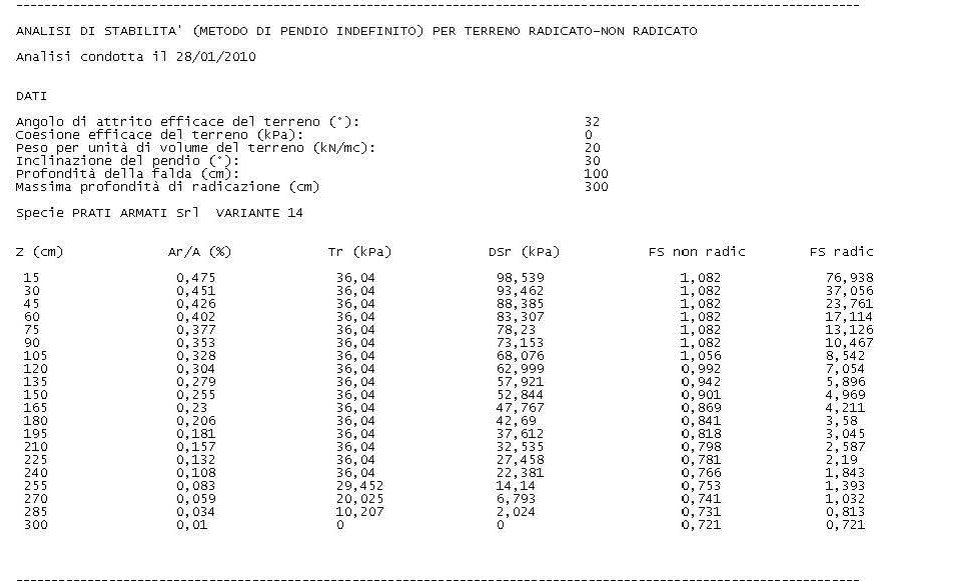
Figura 2. Output (parziale) del codice Prati_Armati@UNIPG
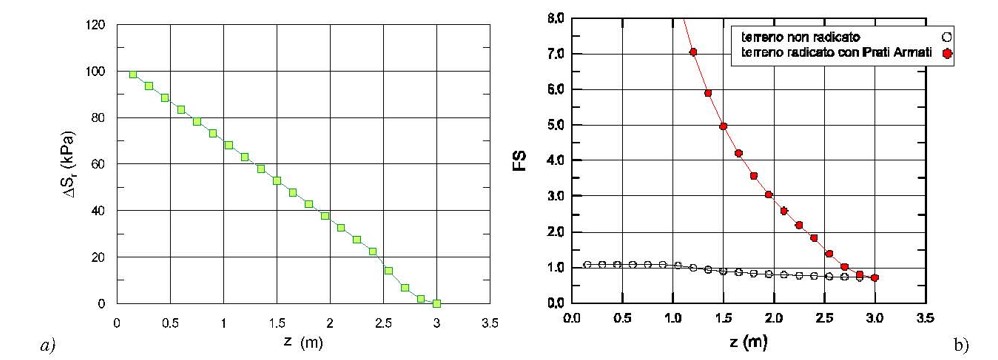
Figura 3.a) Incremento di resistenza a taglio offerto dalle radici, DSr in funzione della prof. z; b) Coefficiente di sicurezza: confronto tra terreno non radicato e radicato con Prati Armati (v. esempio Figura 2)
Valutazione del coefficiente di sicurezza per lo schema di pendio indefinito
Secondo un approccio convenzionale, il coefficiente di sicurezza FS può essere calcolato tramite:
con α angolo di inclinazione del pendio, rispetto all’orizzontale e Ds, profondità della superficie di scorrimento dal piano campagna. I risultati dei calcoli vengono restituiti in output in funzione della profondità per lo strato di terreno radicato, sia in forma tabellare (come file di testo) che in forma grafica, come illustrato nelle Figure 2, 3e 4 per un esempio numerico.
Conclusioni
Allo stato attuale, alcuni aspetti del processo sono ancora trattati in modo empirico. Nel prosieguo della ricerca, si intenderà inoltre completare e perfezionare alcuni moduli del codice non ancora pienamente soddisfacenti dal punto di vista numerico.
Per visionale l’articolo completo pubblicato clicca qui
RIFERIMENTI BIBLIOGRAFICI
Allen, R.G., Pereira L.S., Raes D., Smith M., 1998. Crop evapotranspiration. Guidelines for computing crop water requirements. Irrigation and Drainage Paper 56, FAO, Rome, Italy, 300 p.
Bischetti G.B., Bonfanti F., Greppi M., 2001. Misura della resistenza a trazione delle radici: apparato sperimentale e metodologia d’analisi. Quaderni di Idronomia Montana, 21/1, 349-360.
Bonfanti F., Bischetti G., 2001. Resistenza a trazione delle radici e modello di interazione terreno – radici. Istituto di Idraulica Agraria, Milano – Rapporto interno.
Feddes, R.A., 1987. Crop factors in relation to making reference crop evapotranspiration. In ‘Evaporation and weather’, TNO Committee on Hydrological Research, 39, p. 33-46.
Fredlund, D. G., and Xing A., 1994. Equations for the soil-water characteristic curve. Canadian Geotechnical Journal, 31: 521-532.
Fredlund, D.G., Xing, A., Fredlund, M.D., and Barbour, S.L. 1996. The relationship of the unsaturated soil shear strength to the soil-water characteristic curve. Canadian Geotechnical Journal, 33: 440-448.
Gray D. H., Ohashi H. (1983), Mechanics of fiber reinforcement of sand. Journal of Geotechnical Engineering Division ASCE.
Rassam D.W., Cook F., 2002. Predicting the shear strength envelope of unsaturated soils. Geotechnical Testing Journal, Technical Note, 25: 215-220.
Richards, L.A., 1931. Capillary conduction of liquids through porous medium. Physics, Vol. 1.
Van Genuchten, M. Th., 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils.
Soil Science Society of America Journal, 44: 892-898.
Vanapalli, S.K., Fredlund, D.G., Pufahl, D.E., Clifton, A.W., 1996. Model for the prediction of shear strength with respect to soil suction. Canadian Geotechnical Journal, 33: 379-392.
Vidal, Henri., 1969. The principle of reinforced earth. Highway Research Record no. 282, p. 1-16. Highway Research Board, Nat. Res. Coun., Washington D.C.
Waldron LJ, 1977. The shear stress resistance of root-permeated homogeneous and stratified soil. Soil Science Society of America Proceedings, 41:843-849.

 Prati Armati Srl
Prati Armati Srl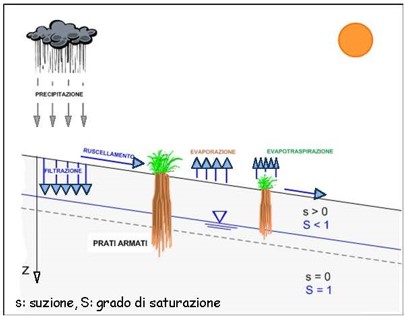










 Prati Armati Srl
Prati Armati Srl

